2025-05-13：第 K 大的完美二叉子树的大小。用go语言，给定一棵二叉树的根节点 root 以及一个整数 k，要求找出第 k 大的满足“完美二叉树”条件的子树的节点数量。这里的“完美二叉树”指的是这样的子树：其所有叶子节点处于同一深度，且每个非叶子节点都有且仅有两个子节点。如果不存在满足条件的第 k 大子树，则返回 -1。

树中的节点数目在 [1, 2000] 范围内。

1 <= Node.val <= 2000。

1 <= k <= 1024。

输入： root = [5,3,6,5,2,5,7,1,8,null,null,6,8], k = 2。

输出： 3。

解释：

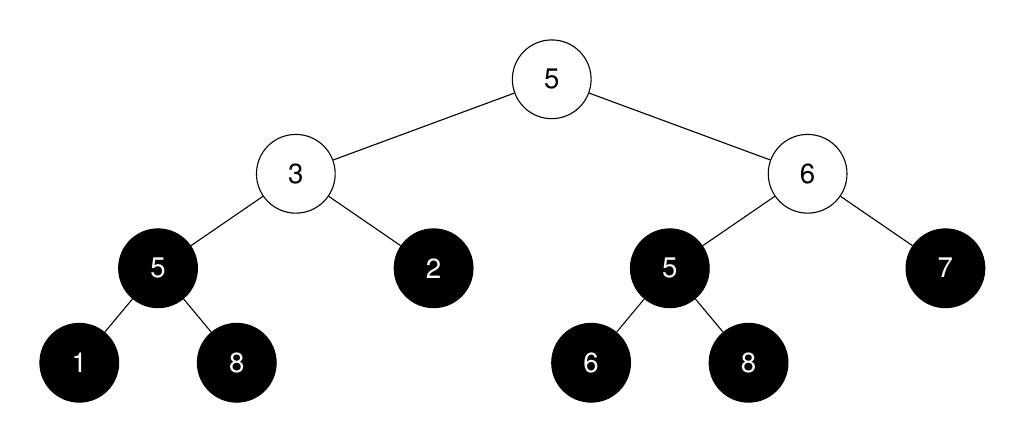
完美二叉子树的根节点在图中以黑色突出显示。它们的大小按非递增顺序排列为 [3, 3, 1, 1, 1, 1, 1, 1]。

第 2 大的完美二叉子树的大小是 3。

题目来自leetcode3319。

解题思路

1. 遍历所有可能的子树

我们需要检查二叉树中的每一个子树，判断它是否是“完美二叉树”，并记录所有符合条件的子树的节点数量。

2. 判断子树是否是完美二叉树

• 递归检查子树的结构：
  • 如果当前节点是 nil，则返回 -1（表示空树）。
  • 递归检查左子树和右子树的高度。
  • 如果左子树或右子树不是完美二叉树（返回 -2），或者左右子树的高度不相等，则当前子树不是完美二叉树，返回 -2。
  • 否则，当前子树是完美二叉树，返回其高度（左子树高度 + 1）。
• 记录完美二叉树的节点数量：
  • 完美二叉树的节点数量可以通过高度计算：节点数量 = 2^(h+1) - 1（其中 h 是高度）。
  • 使用一个数组 cnt 统计不同高度的完美二叉树的数量（cnt[i] 表示高度为 i 的完美二叉树的数量）。

3. 统计所有完美二叉树的节点数量

• 遍历 cnt 数组，从高到低计算每种高度的完美二叉树的节点数量（1, 3, 7, 15, ...）。
• 如果某个高度的完美二叉树数量 c 大于等于 k，则返回该高度的节点数量。
• 否则，k -= c，继续检查更小的高度。

4. 处理边界情况

• 如果遍历完所有高度后 k 仍然大于 0，说明不存在第 k 大的完美二叉子树，返回 -1。

---

详细步骤

1. 初始化统计数组 cnt：

   • cnt 是一个长度为 10 的数组（因为树的最大高度不超过 10，节点数 ≤ 2000）。

2. 递归遍历子树：

   • 从根节点开始，递归检查每个子树是否是完美二叉树。
   • 如果子树是完美二叉树，则更新 cnt 数组（cnt[height]++）。

3. 计算第 k 大的子树大小：

   • 从最大可能的高度（len(cnt)-1）开始遍历 cnt 数组。
   • 对于每个高度 i，计算该高度的完美二叉树的节点数量 size = 2^(i+1) - 1。
   • 如果 cnt[i] >= k，则 size 就是第 k 大的子树大小。
   • 否则，k -= cnt[i]，继续检查更小的高度。

4. 返回结果：

   • 如果找到符合条件的子树，返回其大小。
   • 否则，返回 -1。

---

时间复杂度和空间复杂度

时间复杂度

• 递归遍历所有子树：每个节点最多被访问一次，因此时间复杂度为 O(N)，其中 N 是树的节点数（N ≤ 2000）。
• 统计和计算第 k 大的子树：cnt 数组的长度是固定的（最多 10），因此这部分的时间复杂度是 O(1)。
• 总时间复杂度：O(N)。

空间复杂度

• 递归栈空间：最坏情况下（树退化为链表），递归深度为 O(N)。
• 统计数组 cnt：固定大小为 10，O(1)。
• 总空间复杂度：O(N)（递归栈空间占主导）。

---

总结

1. 递归遍历所有子树，判断是否是完美二叉树。
2. 统计不同高度的完美二叉树的数量。
3. 从高到低计算第 k 大的子树大小。
4. 时间复杂度 O(N)，空间复杂度 O(N)。

Go完整代码如下：

package main

import (
	"fmt"
)

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

func kthLargestPerfectSubtree(root *TreeNode, k int) int {
	cnt := [10]int{}
	var dfs func(*TreeNode) int
	dfs = func(node *TreeNode) int {
		if node == nil {
			return -1
		}
		leftH := dfs(node.Left)
		rightH := dfs(node.Right)
		if leftH == -2 || leftH != rightH {
			return -2 // 不合法
		}
		cnt[leftH+1]++
		return leftH + 1
	}
	dfs(root)

	for i := len(cnt) - 1; i >= 0; i-- {
		c := cnt[i]
		if c >= k {
			return 1<<(i+1) - 1
		}
		k -= c
	}
	return -1
}

func main() {
	root := &TreeNode{Val: 5}
	root.Left = &TreeNode{Val: 3}
	root.Right = &TreeNode{Val: 6}
	root.Left.Left = &TreeNode{Val: 5}
	root.Left.Right = &TreeNode{Val: 2}
	root.Right.Left = &TreeNode{Val: 5}
	root.Right.Right = &TreeNode{Val: 7}
	root.Left.Left.Left = &TreeNode{Val: 1}
	root.Left.Left.Right = &TreeNode{Val: 8}
	root.Right.Left.Left = &TreeNode{Val: 6}
	root.Right.Left.Right = &TreeNode{Val: 8}
	k := 2
	result := kthLargestPerfectSubtree(root, k)
	fmt.Println(result)
}

Python完整代码如下：

# -*-coding:utf-8-*-

from typing import Optional

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

def kth_largest_perfect_subtree(root: Optional[TreeNode], k: int) -> int:
    cnt = [0] * 10  # 用于记录不同高度的完美子树数量

    # 返回值：
    # -1 表示空节点
    # -2 表示非法子树（不完美）
    # 其他 >= 0 表示该节点为根的完美子树的高度
    def dfs(node: Optional[TreeNode]) -> int:
        if node is None:
            return -1
        left_h = dfs(node.left)
        right_h = dfs(node.right)
        if left_h == -2 or left_h != right_h:
            return -2
        # 该节点是完美子树根，其高度为 left_h + 1
        cnt[left_h + 1] += 1
        return left_h + 1

    dfs(root)

    # 从大高度往小高度遍历，计算第 k 大的完美子树大小
    for h in reversed(range(len(cnt))):
        c = cnt[h]
        if c >= k:
            # 完美二叉树节点数 = 2^(高度+1) - 1，代码中高度是 h，从0开始
            return (1 << (h + 1)) - 1
        k -= c
    return -1

# 测试代码
if __name__ == '__main__':
    root = TreeNode(5)
    root.left = TreeNode(3)
    root.right = TreeNode(6)
    root.left.left = TreeNode(5)
    root.left.right = TreeNode(2)
    root.right.left = TreeNode(5)
    root.right.right = TreeNode(7)
    root.left.left.left = TreeNode(1)
    root.left.left.right = TreeNode(8)
    root.right.left.left = TreeNode(6)
    root.right.left.right = TreeNode(8)
    k = 2
    result = kth_largest_perfect_subtree(root, k)
    print(result)